本記事では、圧縮性流体のノズルやオリフィスなどの絞りにおけるチョーク流れ(choked flow)について、数式の背景と物理的意味を重視して解説します。単なる公式暗記ではなく、「なぜそうなるのか」「設計や計算でどこに注意すべきか」を理解することを目的とします
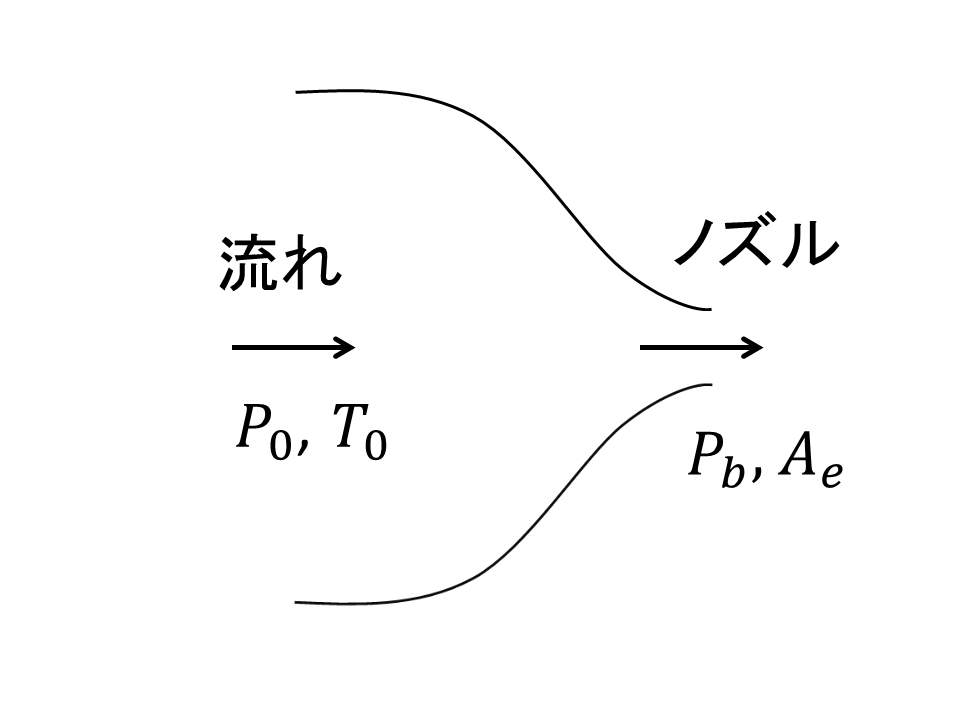
チョーク流れとは何か
定義
チョーク流れとは、ノズルやオリフィスなどの**最小断面(スロート)において、流速が音速(マッハ数 M = 1)**に達し、それ以上 下流圧力を下げても質量流量が増加しなくなる状態を指します。
このとき、流量は上流側の状態(圧力・温度)と開口面積によってのみ決まり、下流の圧力や温度には依存しません。
実務で問題になる場合
- 空気や窒素、酸素、蒸気など圧縮性流体のノズルやオリフィス流量計算
- 安全弁・リリーフ弁の容量計算
- ノズルやオリフィス流量の上限評価
「下流圧力をどれだけ下げても流量が増えない」という現象は、現場では流量が頭打ちになるとして経験的に知られています。
なぜ音速が関係するのか?
音速とは何か
音速とは、圧縮性流体中を圧力変動(情報)が伝わる速度です。流体が音速未満で流れている場合、下流で起きた圧力変化は上流へ伝播します。
情報が上流に伝わらなくなる瞬間
流速が音速に達すると、
- 下流からの圧力変動が
- 上流へ伝わらなくなる
状態になります。
つまり、スロートで音速になると、上流は下流の状態を「知ることができない」このため、下流圧力をさらに下げても、上流条件や流量は変化せず、流量が固定(チョーク)されます。
チョークが発生する条件
臨界圧力比
チョーク流れが発生するかどうかは、一次圧と背圧(二次圧)の比で決まります。理想気体・等エントロピー流れを仮定すると、臨界圧力比は次式で与えられます。
$$\frac{P_b}{P_0}=\left(\frac{2}{γ+1}\right)^\frac{γ}{γ-1}$$
\(P_b\)は背圧(二次圧)、\(P_0\)は一次圧を表し、単位は\(\mathrm{[Pa \cdot abs]}\)絶対圧です。\(γ\)は比熱比です。例えば空気なら\(γ=1.4\)です。したがって、空気の臨界圧力比は
$$\left(\frac{P_b}{P_0}\right)=0.528$$
となります。一次圧と背圧(二次圧)の比がこの値以下になると、チョーク流れ(音速流れ)になります。
質量流量が一定になる理由
流れが音速に達すると、
- これ以上流速を上げられない。
- 密度低下で帳尻を合わせようとする。
- 結果として質量流量は一定。
となります。この「流速は上げられない」という制約こそが、チョーク流れの本質です。
チョーク流れの質量流量式
$$\dot{m}^*=C_d A_e P_0\sqrt{\frac{\gamma}{R T_0}\left(\frac{2}{\gamma+1}\right)^{\frac{\gamma+1}{\gamma-1}}}$$
\(\dot{m}^*\):質量流量\(\,\mathrm{[kg/s]}\) チョーク流れの条件に\(*\)を付けています。
\(C_d\):流量係数\(\,\mathrm{[-]}\)
\(A_e\):縮流部の流路面積\(\,\mathrm{[m^2]}\)
\(P_0\):一次圧\(\,\mathrm{[Pa \cdot abs]}\)
\(R\):気体定数\(\,\mathrm{[J/(kg \cdot K)]}\)
\(T_0\):一次側温度\(\,\mathrm{[K]}\)
\(\gamma\):比熱比\(\,\mathrm{[-]}\)
※等エントロピー、理想気体を仮定し、絞り部分は十分短いとします。
実務上の注意
- 小径オリフィスでは粘性損失が無視できない。
- 流量係数で調整する必要がある。
- 流量係数は必ず実験値またはメーカー値を使う。
- 蒸気では湿り度・非理想性の影響が出る。
よくある誤解
- 「二次圧力下げれば無限に流れる」→ 誤り。チョーク流になるとそれ以上質量流量は増えません。
- 「チョーク=危険」→ 誤り。安全弁や流量制限では意図的に使う現象です。
設計での考え方
- チョークする前提で最大流量を決める。
- 非チョーク域での制御が必要か切り分ける。
- 下流条件に期待しすぎない設計をする。
まとめ
- チョーク流れは音速が上限になる現象。
- 本質は「下流情報が上流に伝わらない」こと。
- チョーク流れの流量は以下の条件で決まります。
- 流体の種類
- 上流条件(圧力と温度) ※下流側の状態の影響は受けません。
- 開口面積
- 流量係数(ノズルやオリフィスの形状による。)
- 設計では最大流量評価の基準になる。
関連記事


コメント